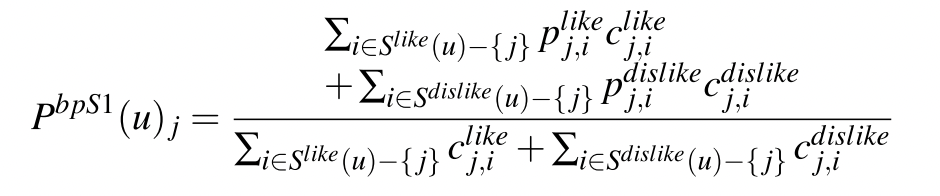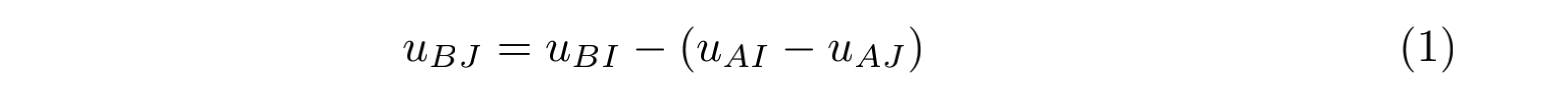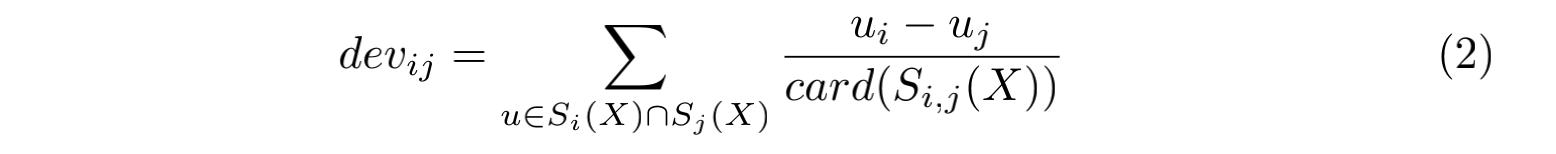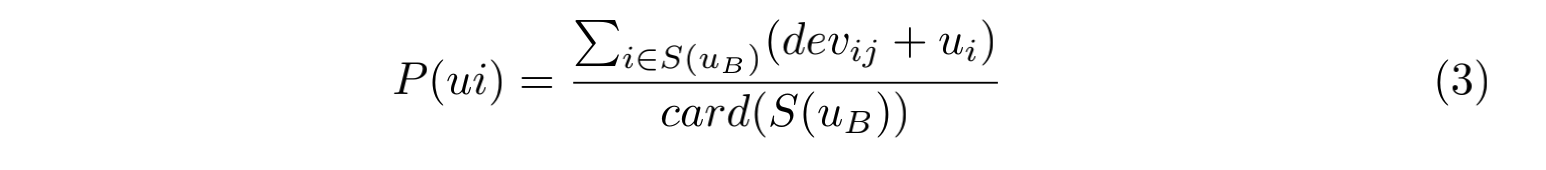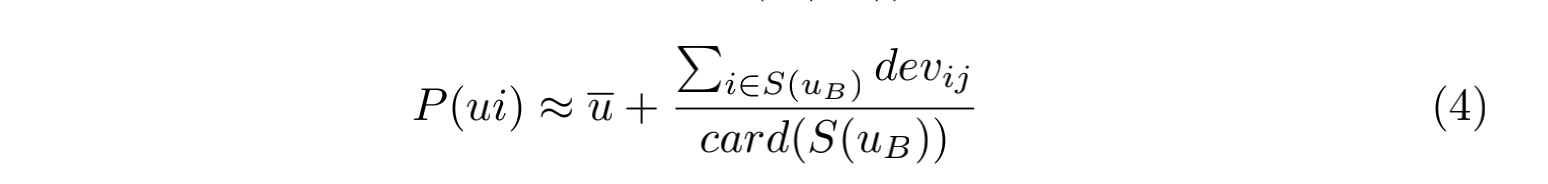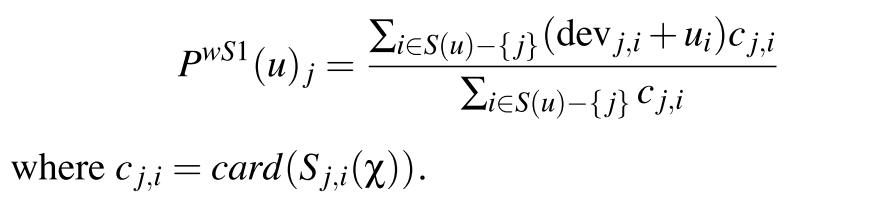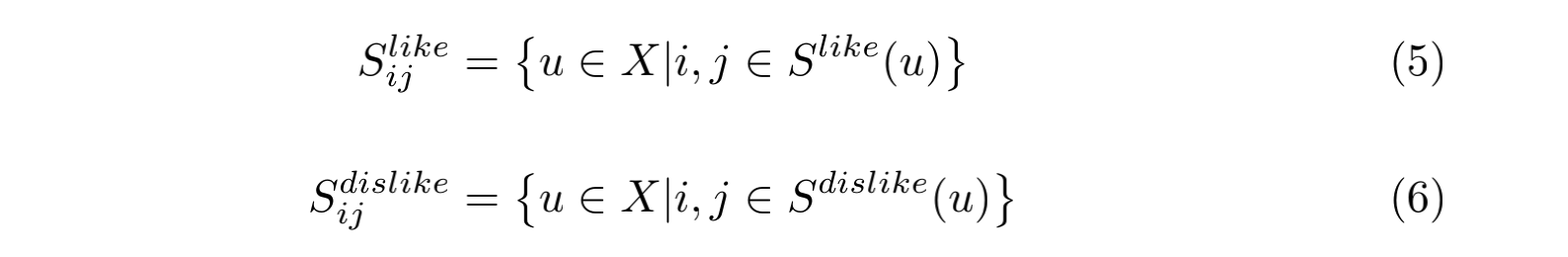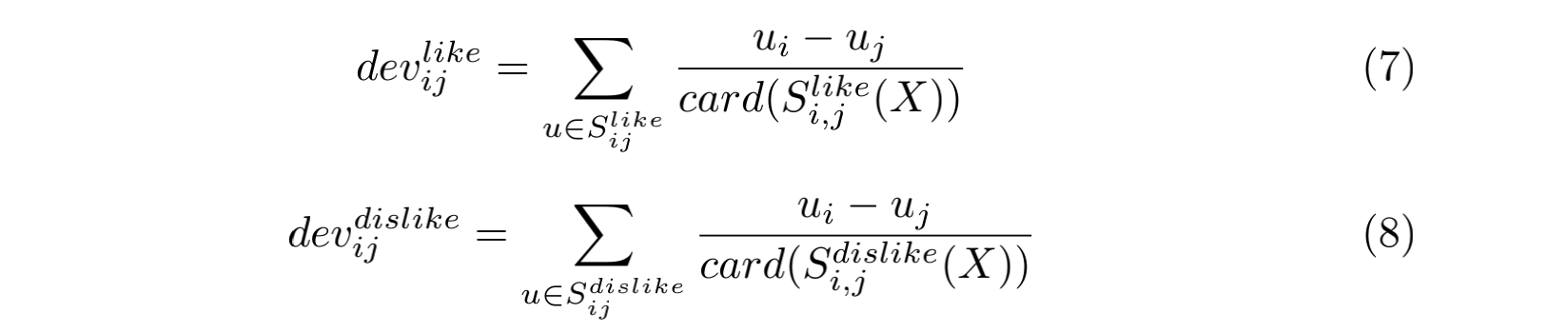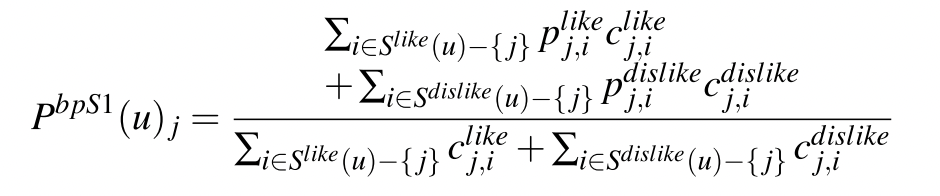Slope One 是一系列应用于协同过滤的算法的统称。由 Daniel Lemire和Anna Maclachlan于2005年发表的论文中提出。

Slope One 方案

比方说我们有两个用户 $UserA$ 和 $UserB$ 以及他们对两个物体 $ItemI$ 和 $ItemJ$ 的评分。

	$Item$ $i$	$Item$ $j$
$UserA$	1.0	1.5
$UserB$	2.0	？

我们可以预测 $UserB$ 对 $ItemJ$ 的分数是：

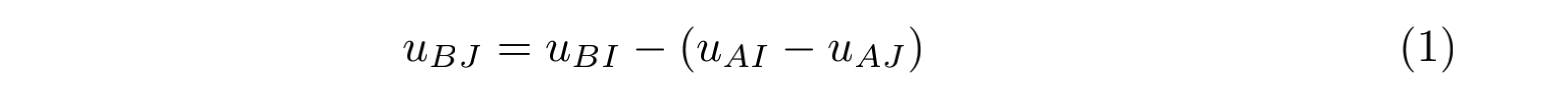
其中 $u$ _BI 表示 $UserB$ 对 $ItemI$ 的评分。带入可得： $u$ _BI = 2.0 - (1.0 - 1.5) = 2.5

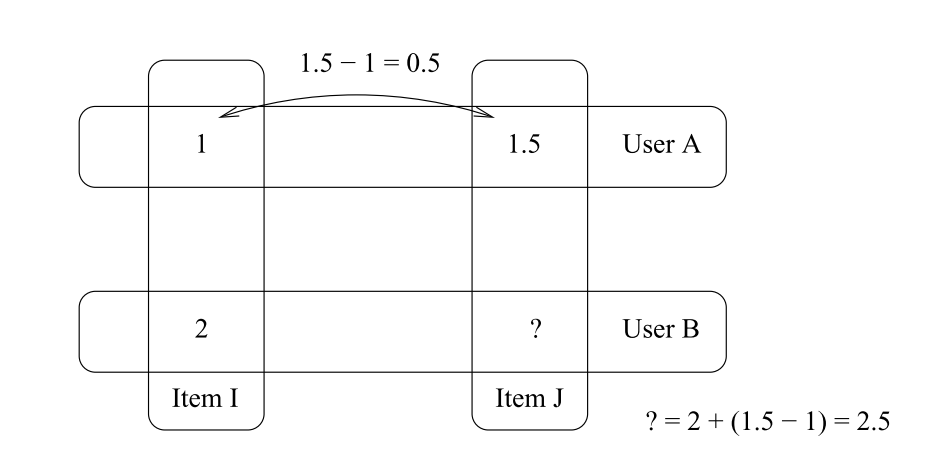
我们可以将数据集扩展一下：

	$Item$ $i$	$Item$ $j$	$Item$ $k$	$Item$ $l$	$Item$ $m$	$\overline{u}$
$UserA$	1.5	1.0	1.2	1.0	2.0	1.34
$UserB$	2.0	?	4.0	2.1	4.0	3.03
$UserC$	4.0	2.1	3.5	3.1	2.6	3.06
$UserD$	3.0	2.3	2.0	2.1	1.0	2.08
$UserE$	1.0	2.4	2.0	1.1	3.0	1.90

基于上述的方法我们可以得到「物品之间的评分偏差矩阵」：

	$Item$ $i$	$Item$ $j$	$Item$ $k$	$Item$ $l$	$Item$ $m$
$Item$ $i$	-	0.425	-0.24	0.42	-0.22
$Item$ $j$	-0.425	-	0.225	0.125	-0.2
$Item$ $k$	0.24	-0.225	-	0.66	0.02
$Item$ $l$	-0.42	-0.125	-0.66	-	-0.67
$Item$ $m$	0.22	0.2	-0.02	0.67	-

物品的评分偏差计算方法如下：

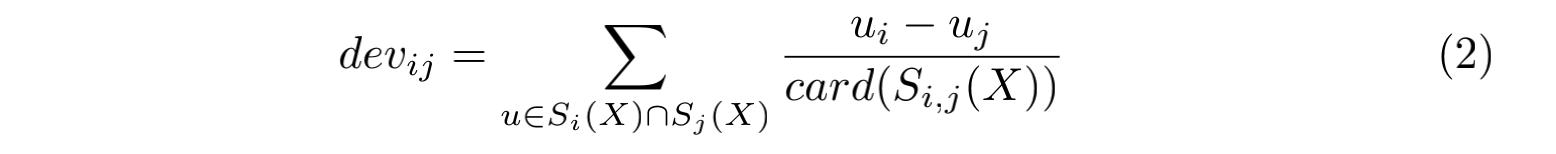
其中 $dev_{ij}$ 表示 $Item$ $i$ 与 $Item$ $j$ 之间的偏差， $S_i(X)$ 表示训练集 $X$ 中所有包含物品 $i$ 的评分数组， $card(S)$ 表示在集合 $S$ 中元素的个数， $u_i$ 表示用户对物品 $i$ 的评分。

再根据这个偏差，我们可以预测用户 $B$ 对物品 $j$ 的评分：

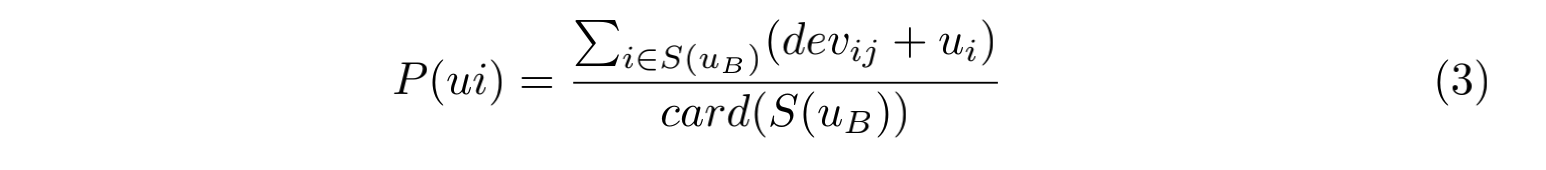
化简可得：

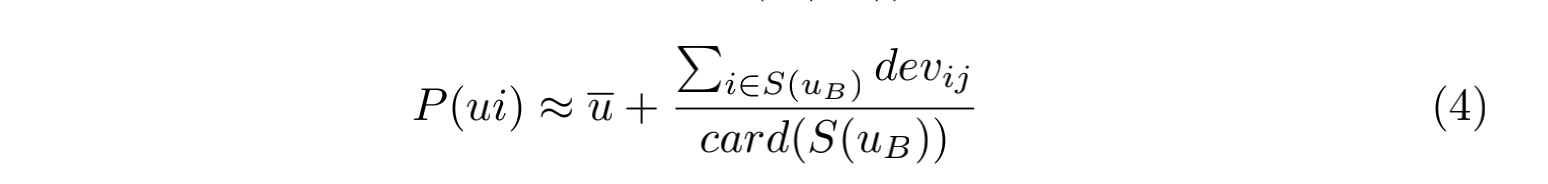
简而言之，Slope One 通过「共同用户」物品的平均打分，来预测某用户下一物品的打分。

加权的 Slope One 方案

从「评分预测」来看，打分用户数对评分偏差没有影响。也就是说，不管有多少用户给某两个物品打分，我们只是取所有物品评分差的平均值。比如我们有 $UserA$ 的打分表：

	$Item$ $i$	$Item$ $j$	$Item$ $k$
$UserA$	3.5	2.4	?

$Item$ $i$ 和 $Item$ $j$ 的出现次数与评分分差：

	$Item$ $i$	$Item$ $j$
$c$	1000	30
$dev$	0.5	0.2

按 Slope One 算法来计算的话打分为： $P(u_k)$ = (3.5 + 2.4) / 2 + (0.5 + 0.2) / 2 = 3.3

那么我们可以对评分分差「加权」：

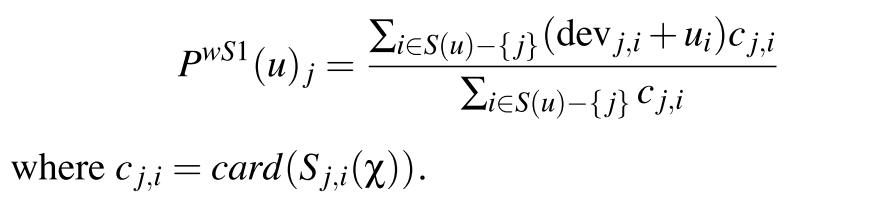
这样计算结果就是： $P(u_k)$ = $\frac{(1000*(3.5+0.5) + 30*(2.4+0.2))}{1000+30}$ = 3.96

在上面这个例子我们发现频繁出现的部分对于预测的影响过于强大。我们将使用新的方法把数据集分成两个部分：

我们认为，只有两个用户对某物品的评分一致的时候，这个评分才是有效的（两个用户对同一物品的评价都是喜欢或者都是不喜欢的时候）。其实这个时候我们开始简单地考虑了用户之间的相似度（都喜欢或者都不喜欢同一物品可以侧面反映用户的相似度）。

我们还是以之前的数据集为例：

	$Item$ $i$	$Item$ $j$	$Item$ $k$	$Item$ $l$	$Item$ $m$	$\overline{u}$
$UserA$	1.5	1.0	1.2	1.0	2.0	1.34
$UserB$	2.0	?	4.0	2.1	4.0	3.03
$UserC$	4.0	2.1	3.5	3.1	2.6	3.06
$UserD$	3.0	2.3	2.0	2.1	1.0	2.08
$UserE$	1.0	2.4	2.0	1.1	3.0	1.90

对于用户 $A$ 来说:

所以我们可以把物品的评分合集划分成两个部分：

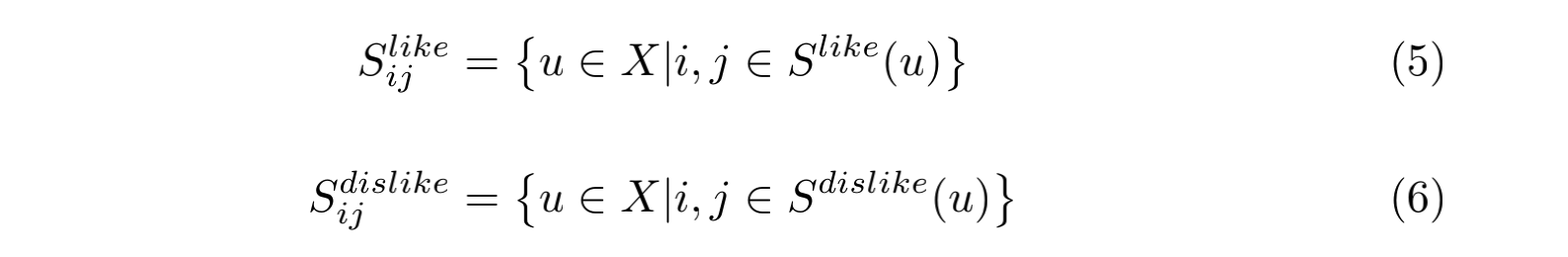
同理，偏差值的计算也有两部分：

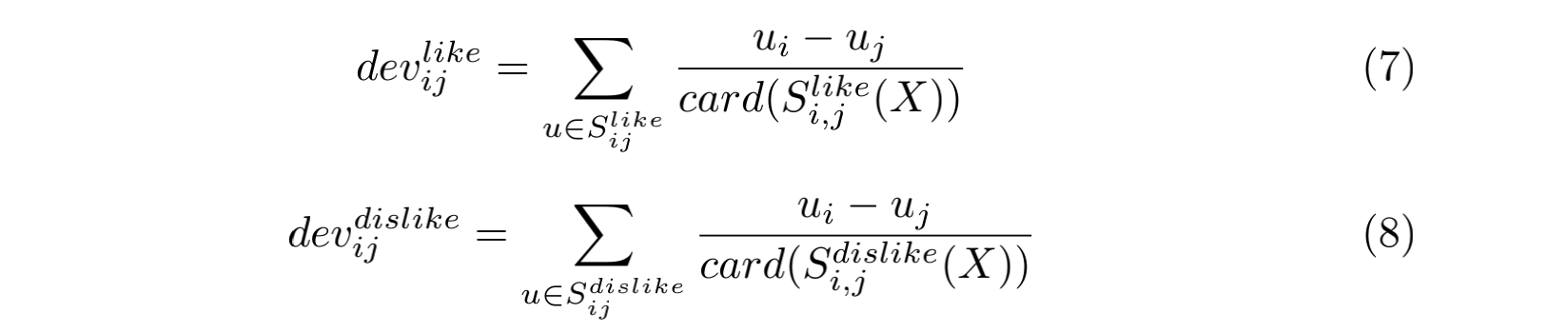
则预测分数的时候我们需要考虑喜欢和不喜欢两个偏差